Ficha formativa para o 10.º ano - Poliedros

Poliedros são sólidos geométricos cujas faces são superfícies planas.

Os elementos de um poliedro são as faces, os vértices e as arestas. As faces de um poliedro são polígonos.

 

Ângulos internos de um polígono regular

 

Vamos deduzir uma expressão que nos dê a amplitude de cada um dos ângulos internos de um polígono regular.

Para isso analisemos alguns casos.

·         Triângulo equilátero

Se considerarmos as bissectrizes de cada um dos ângulos internos do triângulo,

elas encontram-se num ponto a que se chama incentro.

360°: 3 = 120° é a amplitude dos ângulos AIO, AIE e EIO

180° – 120° = 60° = IÂO + AÔI

Como IÂO = AÔI = 30° cada um dos ângulos internos do triângulo tem de amplitude 60°

 

·         Quadrado

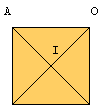
360°: 4 = 90° é a amplitude de cada um dos ângulos formados pelas diagonais do quadrado.

180° – 90° = 90° = IÂO + AÔI

Como IÂO = AÔI = 45° cada um dos ângulos internos do quadrado mede 90°.

 

·         Pentágono

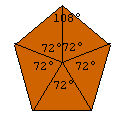
360°: 5 = 72°

180° – 72° = 108° é soma das amplitudes dos outros dois ângulos de cada triângulo.

Como estes ângulos são iguais (o triângulo é isósceles), a amplitude de cada

ângulo interno do pentágono é 108°.

……

 

·         No caso geral de um polígono de n lados, temos:

360°: n

180° – 360°: n

Portanto, a amplitude de cada um dos ângulos internos é

Um poliedro diz-se regular se as faces são todas geometricamente iguais e em cada vértice o número e a disposição dos polígonos regulares são iguais.

São 5 os poliedros regulares:

Tetraedro	Planificação
Cubo
Octaedro
Dodecaedro
Icosaedro

 

Estes 5 sólidos também são chamados sólidos platónicos, em homenagem ao filósofo grego Platão (400 a.C.). Os gregos associavam aos poliedros regulares elementos da Natureza.

 

 

Porque é que só existem 5 poliedros regulares?

Num poliedro, o número mínimo de faces que se unem num vértice são 3.

Se num vértice juntarmos:

 

·         3 triângulos equiláteros, a soma das amplitudes dos ângulos que rodeiam cada vértice é 3x60° = 180° ––> Tetraedro

·         4 triângulos equiláteros, a soma das amplitudes dos ângulos que rodeiam cada vértice é 4x60° = 240°––>Octaedro

·         5 triângulos equiláteros, a soma das amplitudes dos ângulos que rodeiam cada vértice é 5x60° = 300°––>Icosaedro

·         6 triângulos equiláteros, a soma das amplitudes dos ângulos que rodeiam cada vértice é 6x60° = 360°. Neste caso não poderíamos construir um sólido mas sim uma superfície plana.

·         3 quadrados, a soma das amplitudes dos ângulos que rodeiam cada vértice é 3x90° = 270°––>Cubo

·         4 quadrados, a soma das amplitudes dos ângulos que rodeiam cada vértice é 4x90° = 360°. °. Neste caso também não poderíamos construir um sólido mas sim uma superfície plana.

·         3 pentágonos, a soma das amplitudes dos ângulos que rodeiam cada vértice é 3x108° = 324°––>Dodecaedro

Não é possível construir mais poliedros regulares.

Arestas, faces e vértices

1) Tetraedro regular tem 4 faces (triângulos equiláteros).

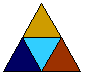
4 triângulos têm: 4x3 = 12 vértices 

4x3 = 12 arestas

Mas em cada vérticedo tetraedro "encontram-se"3 triângulos, logo o tetraedro tem 12:3 = 4 vértices.

Numa aresta do tetraedro "encontram-se" 2 triângulos, assim o tetraedro tem 12:2 = 6 arestas.

Seguindo um raciocínio análogo, complete:

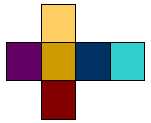
2) Um cubo tem ……faces que são quadrados. 

Cada quadrado tem … vértices e … arestas. Logo … quadrados têm … vértices e … arestas.

Mas em cada vértice do cubo "encontram-se" … quadrados, logo o cubo tem ……… = … vértices.

E numa aresta "encontram-se" … quadrados, assim o cubo tem …… = … arestas.

3) No caso do octaedro, temos:

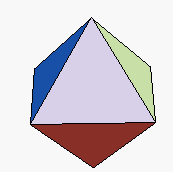
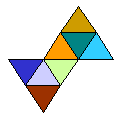
… triângulos

Como em cada vértice do octaedro "se encontram" … vértices, logo ele tem … vértices.

Numa aresta do octaedro "encontram-se" … arestas, portanto o octaedro tem … arestas.

4) No caso do dodecaedro, temos:

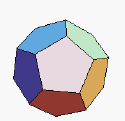
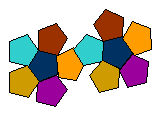
… pentágonos

 

Como em cada vértice do dodecaedro "se encontram" … vértices, logo ele tem … vértices.

Numa aresta do dodecaedro "encontram-se" … arestas, portanto o dodecaedro tem … arestas.

5) No caso do icosaedro, temos:

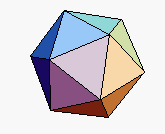
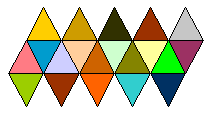
… triângulos

 

Como em cada vértice do icosaedro "se encontram" … vértices, logo ele tem … vértices.

Numa aresta do icosaedro "encontram-se" … arestas, portanto o icosaedro tem … arestas.

 

Complete o quadro seguinte:

Poliedros Regulares	Nº de Faces F	Nº de Vértices V	Nº de Arestas A	F + V	A + 2
Tetraedro
Cubo
Octaedro
Dodecaedro
Icosaedro

 

Comparando as duas últimas colunas, podemos ver que em qualquer destes poliedros F + V = A + 2.

Esta relação é conhecida como regra de Euler:

"Num poliedro o número de faces mais o número de vértices é igual ao número de arestas mais dois".

Chama-se centro de um poliedro regular ao ponto equidistante dos vértices, das faces e das arestas.

Chama-se dual de um poliedro regular ao poliedro cujas arestas se obtêm unindo os centros das faces consecutivas do poliedro dado.

Podemos concluir que o número de vértices de um poliedro é igual ao número de faces do poliedro dual.

Complete o quadro:

 

 

Utilize o endereço www.fc.up.pt/atractor/mat/duais.html para ver poliedros duais.