|
|
|
Condições
no espaço
I
Num
referencial cartesiano Oxyz foi representado o cubo [OEFGDABC] de medida
do comprimento da aresta igual a 6.
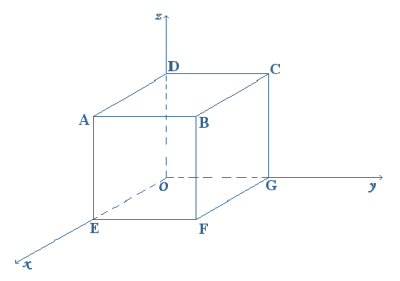
De acordo com
a figura:
a) Indica as
coordenadas dos vértices do cubo.
b) Escreve
uma equação para cada um dos planos que contêm as faces do cubo.
c) Escreve
uma condição que represente a face [EFBA] do cubo.
d) Escreve
uma condição que represente a recta OE. Como representar a aresta [OE] do cubo
através de uma condição no espaço?
d1) E a recta OF? E a aresta [OF]
do cubo?
d2) E a recta BF? E a aresta [BF]
do cubo?
e) As
coordenadas dos pontos A’, B’, C’ e D’ simétricos dos pontos A, B, C e D,
respectivamente, em relação ao plano OEF.
f) As
coordenadas do ponto B’’ simétrico do ponto B em relação ao eixo Oz.
g) As
coordenadas do ponto A’’ simétrico do ponto A em relação ao plano yOz.
h) As
coordenadas do ponto F’’ simétrico do ponto F em relação a Origem do
referencial.
i) Indica as
coordenadas de um ponto H equidistante dos vértices do cubo O e G. Quantas
soluções é possível encontrar?
j) Indica as
coordenadas de um ponto I do eixo das cotas sabendo que o ângulo entre as
rectas EO e EI é de 60º.
k) Qual a
medida do comprimento da diagonal [DF] do cubo?
II
Num
referencial cartesiano Exyz foi representado o cubo [ OEFGDABC] de
medida do comprimento da aresta igual a 8.
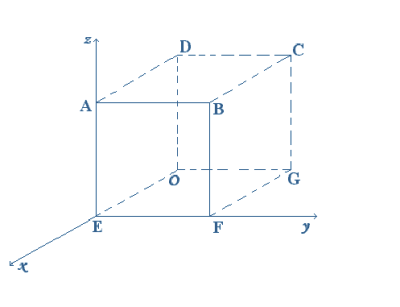
De acordo com
a figura:
a) Indica as
coordenadas dos vértices do cubo.
b) Escreve
uma equação para cada um dos planos que contêm as faces do cubo.
c) Escreve
uma condição que represente a face [EFBA] do cubo.
d) Escreve
uma condição que represente a recta AB. Como representar a aresta [ AB] do cubo
através de uma condição no espaço?
e) As
coordenadas do ponto A’’ simétrico do ponto A em relação ao plano OEF.
f) As
coordenadas do ponto B’’ simétrico do ponto B em relação ao eixo Ez.
g) As
coordenadas do ponto C’’ simétrico do ponto C em relação ao plano xEz.
h) As
coordenadas do ponto F’’ simétrico do ponto F em relação a Origem do
referencial.
i) Indica uma
condição que represente o conjunto de pontos do espaço equidistante dos
extremos do segmento [ EF] .
j) Indica uma
condição que represente o conjunto de pontos do espaço pertencentes a secção
feita por um corte de um plano perpendicular ao eixo Ex e que contém o
ponto médio de [ EO] .
k) Indica uma
condição que represente o conjunto de pontos do espaço pertencentes a secção
feita por um corte de um plano perpendicular ao eixo Ez e que contém o
ponto H.
![]()
l) Indica uma
condição que represente o conjunto de pontos do espaço cuja distância ao ponto
E é igual a metade do comprimento do segmento [ EB] .
III
Num
referencial cartesiano Oxyz foi representado o cubo [ ABCDEFGH] de
medida do comprimento da aresta igual a 12. O ponto O representa o centro de
gravidade do cubo.
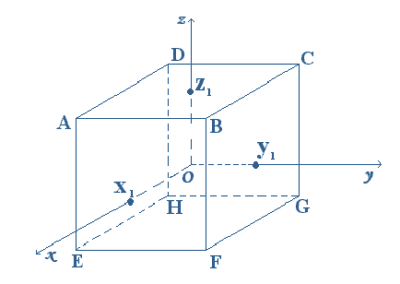
De acordo com
a figura:
a) Indica as
coordenadas dos pontos X1, Y1 e Z1
pertencentes as faces do cubo.
b) Indica as
coordenadas dos vértices do cubo.
c) Escreve
uma equação para cada um dos planos que contêm as faces do cubo.
d) Escreve
uma condição que represente a fase [EFBA] do cubo.
e) Escreve
uma condição que represente a recta AB. Como representar a aresta [AB] do cubo
através de uma condição no espaço?
f) As
coordenadas dos pontos A’, B’, C’ e D’ simétricos dos pontos A, B, C e D,
respectivamente, em relação ao plano OEF.
g) As
coordenadas do ponto B’’ simétrico do ponto B em relação ao eixo Oz.
h) As
coordenadas do ponto C’’ simétrico do ponto C em relação ao plano xOz.
i) As
coordenadas do ponto F’’ simétrico do ponto F em relação a Origem do
referencial.
j) Indica uma
condição que represente o lugar geométrico dos pontos do espaço equidistante
dos extremos do segmento [EF] .
k) Verifica
que o ponto X1 pertende ao plano mediador de [AB] .
l) Indica uma
condição que represente o conjunto de pontos do espaço pertencentes a secção
feita por um corte de um plano perpendicular ao eixo Oz e que contém o
ponto médio de [FY1] .
m) Indica uma
condição que represente o conjunto de pontos do espaço cuja distância ao ponto
O é igual ao comprimento do segmento [OZ1] .